Sentiamo spesso dire che gli scommettitori professionisti fanno uso di complessi strumenti matematici per raggiungere dei risultati favorevoli.
Uno di questi strumenti (neanche poi così complesso, in realtà) è il cosiddetto criterio di Kelly.
John Larry Kelly jr. era uno studioso di Princeton che negli anni ’50 ha pubblicato alcuni studi che si sono rivelati un cardine, negli anni successivi, nella gestione del portafoglio degli investimenti. Ovvero, mediante delle inconfutabili formule matematiche, teorizzava con successo quale fosse la porzione ottimale del proprio budget da impiegare in ogni singolo investimento.
Come è facile immaginare, l’applicazione dei suoi studi nel settore del betting è venuta pressoché subito dopo.
Grazie a lui, infatti, oggi possiamo calcolare quale sia la cifra ottimale da scommettere in ogni scommessa singola.

L’enunciato

Come spiegato nel suo trattato universitario , la formula coniata da Kelly consente allo scommettitore di calcolare l’importo ottimale da puntare tenendo in considerazione la quota offerta dal bookmaker e il proprio personale pronostico. Secondo l’autore, scommettere una cifra maggiore implicherebbe un rischio troppo elevato, mentre scommettere di meno comporterebbe un rendimento più basso e contestualmente genererebbe uno spreco di ‘probabilità’ a proprio favore.
Per ricavare il massimo profitto è necessario stimare la probabilità reale di riuscita della scommessa. È molto importante che questa stima sia più precisa di quella del bookmaker (problema su cui torneremo tra poco, comunque), perché da ciò dipende il successo dal criterio di Kelly.
La puntata ottimale è espressa da una percentuale del proprio budget (o bankroll): per calcolare l’importo della  puntata, è necessario quindi conoscere la quota proposta sull’evento dal bookmaker (Q) e determinare con precisione la probabilità (P) che il proprio pronostico risulti vincente .
La formula di Kelly :
 % del bankroll da scommettere sull’evento = (Q x P-1) / (Q-1)
ossia
(((Quota x (Probabilità/100)) – 1) / (Quota – 1)) x 100

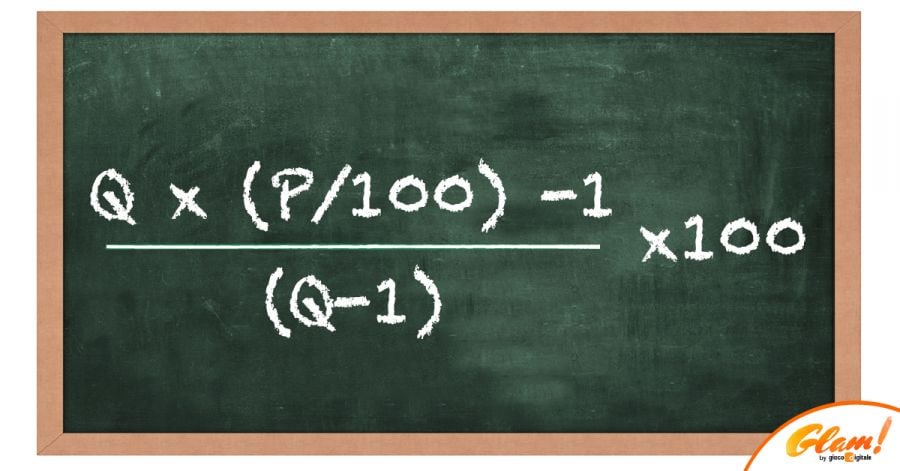
Un esempio pratico

“Si vabbè, ma di matematica non ci capisco niente!”
E’ normale, non ci si allarmi. Ora un esempio pratico ci chiarificherà le idee.
Supponiamo che nella prossima giornata del campionato italiano di Serie A l’ottima Atalanta di Gasperini vada a far visita alla altrettanto agguerrita Sampdoria di Giampaolo.
Il nostro bookmaker di riferimento quota l’1 (cioè la vittoria Samp) a 2.00, il pari a 3,50 e la vittoria esterna a 3,15.
Il giorno prima della partita, però, scopriamo dalla conferenza stampa del mister orobico che a causa di una improvvisa influenza né Ilicic, nè Zapata né tantomeno Toloi (ovvero i calciatori forse più rappresentativi della Dea) prenderanno parte alla trasferta di Marassi; allo stesso tempo, Giampaolo si è professato molto sicuro circa lo stato di forma di Quagliarella e compagni.
Con queste premesse, pensiamo che forse una quota a 2.00 per la vittoria casalinga (corrispondente ad un 50% di concrete possibilità di vittoria) ci sembra un po’ stretto, e personalmente cominciamo a ritenere che forse la Samp possa avere almeno il 60% di possibilità di portare a casa l’intera posta. Percentuale che corrisponderebbe ad una quota pari a 1,65 (data dall’operazione 100/60).
La discrepanza tra 2.00 e 1.65 , col criterio di Kelly, è sfruttabile matematicamente: supponendo che il nostro bankroll scommesse ammonti a 1000 euro, la formula va così applicata:
Kelly% = (2.00×60%-1 / 2.00-1) = 0.2%
Pertanto, se le nostre premesse di stima sono corrette, la cifra ottimale da scommettere è lo 0,2% del proprio bankroll, per cui (seguendo l’esempio sopracitato) vanno scommessi 20 euro sul segno 1.

Considerazioni finali

Il criterio di Kelly consentirà di gestire il proprio budget in maniera efficiente, evitando che si esaurisca nel breve tempo. Ovviamente, questa formula è legata indissolubilmente alla capacità di stimare con precisione l’esatta probabilità percentuale che un determinato avvenimento si verifichi. Infatti, qualora si tenda ad effettuare stime superiori a quelle reali, la percentuale ottenuta mediante la formula risulterà sproporzionata e con il passare del tempo il budget potrebbe esaurirsi. Viceversa, se si effettuano stime inferiori a quelle reali, si otterrebbe un margine di guadagno inferiore rispetto a quello che sarebbe stato ottenibile considerando la probabilità corretta.
Il criterio di Kelly, in definitiva, è uno degli strumenti decisamente più interessanti per la gestione, il mantenimento e lo sviluppo del proprio portafoglio scommesse.
 
 
Tutte le foto utilizzate sono con licenza Creative Commons